Machine Learning in Artificial Intelligence world refers to the collection of methods, that allow machines to perform data analysis and predict future outcomes based on predetermined factors. None of the ML models can predict with 100% accuracy. The accuracy of these predictions depends on multiple factors. One of the factors and among the most important ones is Bias-Variance Tradeoff.
Bias and Variance are the prediction errors that the machine learning model makes when there are fewer data to train from, or too many assumptions a model makes to perfectly train on the training dataset that it fails to predict the test dataset or any unseen data accurately. Bias and variance are one of the ‘must-know’ concepts for every data scientist. Before diving into this, let’s first understand overfitting & underfitting.
Concept of Overfitting & Underfitting
Overfitting and Underfitting in ML models are closely related to Bias and Variance.
Overfitting refers to a scenario when the model tries to cover all the data points present in the given dataset. As a result, the model starts caching noise and inaccurate values present in the dataset and then reduces the efficiency and accuracy of the model. High Variance in the model leads to overfitting. Chances of Overfitting are more with nonparametric and nonlinear models that have more flexibility when learning a target function.
Underfitting is just the opposite of overfitting. The machine learning model is not able to capture the underlying trend of the data or there is less data for training the model. High Bias leads to the underfitting of the ML model.
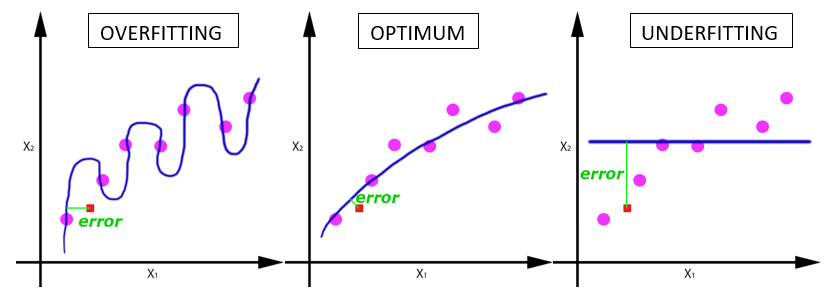
Understanding the Bias & Variance with example
Bias
The bias is known as the difference between the predicted values by ML model and the expected/correct value. Being high in bias, the model generates a large error in training as well as testing data.
Variance
Variance is the opposite of Bias. It defines the model’s sensitivity to fluctuations in the data. If we allow the model to view the data too many times, it will capture almost all the patterns in the data but along with that, it will pick up the noise present in the data which is irrelevant to predict the unseen or test data. This is called ‘high variance’. Here, the model will perform amazingly well on the training data as it will capture all the points, but will fail miserably on test data or unseen data to predict the labels.
Let’s imagine the situations of Bias and Variance in the model through this Bull’s Eye graph:
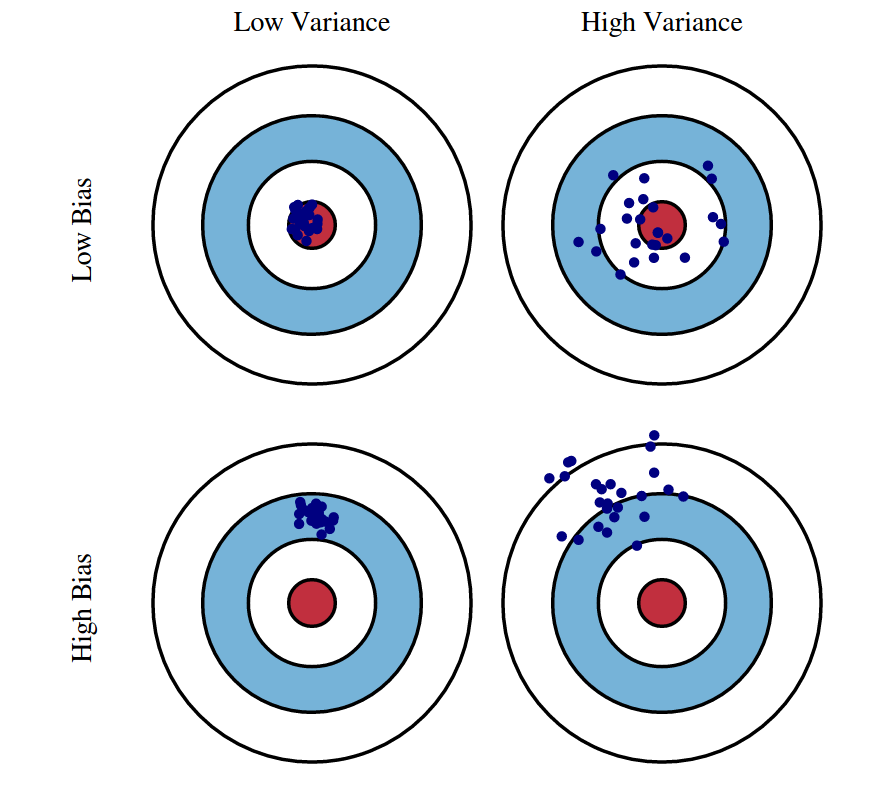
Low-Bias, Low-Variance: The combination is an ideal machine learning model. However, it is not possible practically.
Low-Bias, High-Variance: This is a case of overfitting where model predictions are inconsistent and accurate on average. The predicted values will be accurate(average) but will be scattered.
High-Bias, Low-Variance: This is a case of underfitting where predictions are consistent but inaccurate on average. The predicted values will be inaccurate but will be not scattered.
High-Bias, High-Variance: With high bias and high variance, predictions are inconsistent and also inaccurate on average.
Bias-Variance TradeOff
Now that we understood how Bias and Variance (reducible errors) play roles in the prediction accuracy of the model, let’s figure out how can we minimize both errors to a point where our model makes sense.
One way to achieve this is by controlling the complexity of the model. Simple models tend to have high bias and low variance. Such models can be Linear algos, Parametric algos, Naïve Bayes, etc. While complex models tend to have low bias and high variance. These can be Decision Trees, Nearest Neighbours, Non-Linear algos, and non-parametric algos, etc.
We can use techniques like cross-validation, regularization, and early stopping to balance the trade-off within the model. For example, regression models can be regularized to increase the complexity. And, decision tree model can be pruned to decrease the complexity.
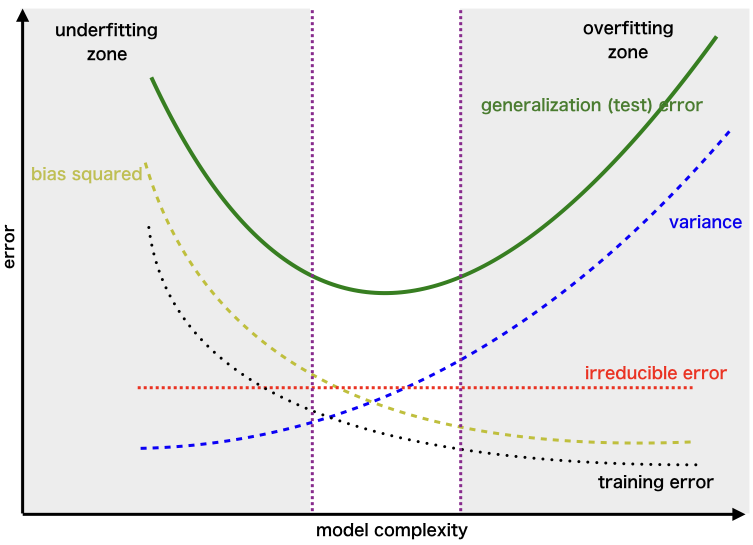
Other techniques to reduce high variance:
- Add more records to training data
- Using Bagging process
Other techniques to reduce high bias
- Add more features to the data
- Using Boosting process
One sign of the good model is that the testing score of the model should be highest and closest to training score. This will provide assurance regarding the minimization of both Bias and Variance errors.
More to read:
- Bias-Variance TradeOff by Vijayakumar Sethu (2007), University of Edinburgh
- A Unified Bias-Variance Decomposition by Pedro Domingos, University of Washington
Please, don’t forget to subscribe newsletter for updates on new articles and upcoming exciting sections.

